几条公关应该懂的理论与规律

我去外面演讲和培训，经常被要求直接说实际的、能操作的干货。

不是说不出来，而是觉得真要这么做了的话，有点害人。

一方面，公关是个几乎没有定式可以套用的领域，你不明白本质上到底怎么回事，一知半解就去执行一些操作，结果很可能就是死得更快；

另一方面，公关做得怎么样，执行决定好坏，思路决定成败。没有成败，哪有好坏。

公关，干的是靠思路解决问题的重脑力劳动。对于公关来说，没有现象，全是本质；没有偶然，全是概率；没有猜测，全是预判；没有兼得，全是权衡。

借助几个理论，讲讲我觉得能够激发公关领域深度思考的东西。没有操作，全是思考。

01信息茧房    

2006年，哈佛大学凯斯·桑斯坦教授在《信息邦》中提出，人类社会存在“信息茧房”现象。教授说，在信息传播中，人们的信息需求从来不是全方位的，只会选择想要的或能使自己愉悦的信息。久而久之，接触的信息就越来越局限，越来越窄，就像蚕吐出来的丝一样，细细密密地把自己包裹起来，最终像一个蚕宝宝一样被限制在“信息茧房”内，失去对其他不同事物的接触机会和了解能力。

当时，这还看着像是一种吓唬人的预测。随着网络信息和人工智能技术的发展，“信息茧房”几乎成了日常现象。无法关闭的“监听”和顶着“智能推送”名义的算法，通过网络接收信息的针对性大大增强，你关注过什么、对什么感兴趣，源源不断地被送到你的眼前。同时，观点看法的分众性明显增强，对同一件事的讨论常常非黑即白，互怼互讥，两极对立，你死我活。

如果我们不去主动突破，只是被动接收的话，不管是正确的还是错误的观念，都会被自己下意识的加强。“信息的自由度空前提高”，这话越看越像是AI战忽局编出来麻痹我们的。

我对信息茧房的态度是，避开。

理由也很简单，本来应该会有3个选择：改变，利用，躲。前2个都弄不了。

首先，没法改变。整体专业水平都不怎么样的公关行业肯定没有能力改变已经成为社会和时代问题的信息茧房状态。

其次，不敢利用。信息茧房人群的行为模式，参见饭圈。粉，黑粉，脱粉反踩，都可以了解一下。       

那么还能选的路，只剩避开。虽然信息茧房是由整体行为模式改变而引发的，但是对于不同话题，信息茧房的收拢程度，区别依然很大。比如，我们讨论吃麻辣烫要不要放醋，余地就比较大；讨论性别、地域、阶级话题，那就基本没有活路。

所以，对于公关来说，要很清楚自家品牌相关信息传递过程中，哪些内容和话题是容易遭遇信息茧房，怎么说都说不通的。而且，不要死磕，多大本事啊，靠几个企业PR在那儿跟社会矛盾死磕。给自己留条活路，说点大家都能明白，也更容易赞同的就好。

不过，即便是在自家品牌相关信息范畴，掌握“哪些内容和话题是容易遭遇信息茧房”，可能很大一部分人已经做不到了。

02幸存者偏差

幸存者偏差这个概念由美国的沃德教授提出，附赠一个有名的打飞机故事：二战时期，需要用统计学研究战机被击中的部位，从而确定哪个部分需要额外加强装甲。对于返航的飞机进行弹痕分析，发现机翼弹孔较多，由此得出应该是加强机翼的装甲防护会更好。而实际上，驾驶舱、油箱和机尾等看上去弹孔不多的部位，一旦中弹，飞机很可能连飞回来的机会都没有了，这就是所谓的“看不见的弹痕最为致命”。

公关领域，幸存者偏差广泛存在，广泛到满地都是，随便说几个：

听身边的人说公司产品好，就觉得产品真的很不错，幸存者偏差；

听竞品公司跳槽来的人，吐槽前司，觉得还是自家公司靠谱，幸存者偏差；

看到朋友圈很多人在发自家海报，觉得形成广泛传播，幸存者偏差；

看到某个话题下面的评论并不激烈，判断风险较小，幸存者偏差。

前面3条比较好理解，我解释下第4条。

同一个话题的不同表达形式，公众反应是不同的。我们每次看到的是对某种形式最敏感的受众在表达看法，还有大量的人没有说话。

他们没在评论里骂你，不代表他们没在心里骂你，也不代表他们不存在。一旦换了传播形式，他们可能就会骂得更凶。因为这次传播骂声不大，判定话题安全，也是上了幸存者偏差的当。

人们经常只会看到经过某种筛选而产生的结果，而没有意识到筛选的过程，从而忽略了被筛选掉的关键信息。

公关要做的是，修正幸存者偏差。就像发现真的需要加固的不是机翼，而是油箱。

为自家产品说好话的同事，是好同事；不知道他们在说好话的公关，不是好公关。

跟前司势不两立的同事，是有前途的同事；不知道他们如果离开一样会说这家公司坏话的公关，不是有前途的公关。

主动在朋友圈转发宣传的同事，是爱公司的同事；不知道即便同事刷屏也是自嗨不代表真的形成有效传播的公关，不是爱公司的公关。

我再说个极端情况。不少人对公关危机处理的理解，还是停留在只要不能“让负面都消失”，直接等于“没什么用”，并且得出一个结论“你看谁谁谁也出过危机，不是还好好的么？”怎么说呢，“还好好的”就是努力处理的结果，是幸存者。因为发生公关危机死掉的，不是不存在，是以你的智商和见识，看不见而已。

现在这种大环境，还在一味自我感觉良好的企业，成为幸存者的概率大大降低。

03伯克松（伯克森）悖论

伯克松悖论当然是伯克松提的。身为医生和统计学家，伯克松有次发现，医院中患有糖尿病的人群中，同时患胆囊炎的人数较少；而没有糖尿病的人群中，患胆囊炎的人数比例则比较高。这是不是可以说明患有糖尿病可以帮助病人减少患胆囊炎的概率？这个结论是错误的。因为统计样本时，只选择了住院的病人，却完全忽略了更多的没有住院的样本。

用比较书面的话来说，当不同个体被纳入研究样本的机会不同时，研究样本中的两个变量 X 和 Y 表现出统计相关，而总体中 X 和 Y 却不存在这种相关性。这就是伯克松悖论。

用人话来说，由于统计数据不够全面，导致两个本来没有特定关系的变量之间，看上去有了貌似紧密的相关关系。

伯克松悖论有几个经典例子：

淹死的人里面，会游泳的比不会游泳的人多，所以会游泳更容易淹死？

戴头盔的摩托车手被送进医院急诊室的比例，远高于不戴头盔的，所以戴头盔反而更不好？

篮球运动比潜水受伤的概率高多了，所以潜水更安全？

伯克松悖论和前面提的幸存者偏差都属于选择偏差。区别在于，幸存者偏差强调的是某一个体特征，柏克松悖论强调的则是两个特征之间是否存在关联。

公关在定调和日常写作中，存在大量柏克松悖论，这是输出内容经不起推敲的重要原因之一。比如，有款零食，低盐低糖无添加剂，宣传点是“更健康”，显然想要建立的是“低盐低糖无添加剂”和“更健康”之间关联。可是，这个取样范围显然是在吃零食人群里，完全忽略不吃零食的群体。当然，不会主动提及不吃零食这个选项。

目前，市面上的0糖宣传，几乎都在运用柏克松悖论。

公关行业不会讨论利用柏克松悖论是否道德。每个人都有自己的标准和选择。

我只想问，作为一个公关，你知不知道自己说出去的东西存在柏克松悖论，经不起推敲和追问。

04大数定律与小数陷阱

大数定律是指，当随机事件发生的次数足够多时，发生的频率才会趋近于预期的概率。

随机抛硬币，出现正面和反面的概率均为 50%，也就是一半正面一半反面。

但如果你抛10次，可能7次正面3次反面，或者8次正面2次反面，并不是5次正面5次反面。

可是，当你抛了几千次、几万次，正面和反面的概率，会趋近于50%。

与大数定律对应的，是小数陷阱。

小数陷阱，也叫赌徒谬误。

随机抛硬币，假如连续 10 次都是正面，很多人就会觉得下一次是反面的概率更高一些。如果是在赌博，就会押注反面，这是典型的“赌徒谬误”。

其实，每次开出正面还是反面，是独立且随机的，并不是前面都是“正面”，后面开“反面”的概率就会高。

如果我说，公关不管怎么费劲心思努力，结果还是充满随机性，是不是很打击大家的积极性？但，事实就是如此。最好的公关也做不到准确判断一个事件经过公众范围传播，会有什么具体结果。越是泛大众，结果越是随机。

公关做的事情，是让概率往有利于自己的方向增加。相当于每天摸一摸硬币的正面。如果我的手特别脏，那么污垢就会留在正面，久而久之，正面变重，抛出正面的概率增加；如果我的手特别粗糙，那么就会磨掉正面的字符，久而久之，正面变轻，抛出反面的概率增加。抛了足够多的次数，大数定律呈现效果也就不再是50%。

这是公关真正发生作用的基本模型。

问题在于，不是每个企业都能活到大数定律发生作用的那一天。小数陷阱一旦连开10把，可能企业就已经差不多要挂了。

小数陷阱对于公关最大的警示在于，开出“正面”，可能是独立且随机的。后面一把是什么，没人知道。今天说你好，明天就骂街，太正常了。

05帕累托法则

帕累托法则诞生于帕累托的花园。如果说也叫二八法则，知道的人会更多。

据说帕累托偶然发现，自己园子里绝大部分的豌豆是由园子里极少部分豌豆荚产生。作为经济学家，他提出了著名的关于意大利社会财富分配的研究结论：20％的人口掌握了80％的社会财富。

这一规律后来在各个领域被广泛观测到：语言中常用词只有500-1000个，剩余的更多词汇使用很少；20%的员工，为公司做出了80%的业绩。帕累托法则也被逐步用来解决时间管理问题、重点客户问题、财富分配问题、资源分配问题、核心产品问题、关键人才问题、核心利润问题、个人幸福问题等。

关联公关，我们可以得出不少相应的推论。比如， 20%的公众制造了80%的舆情，20%的主播获得了80%的播放量，20%的观点占据了80%的传播量。帕累托法则告诉我们的是，要抓住核心和关键性因素。传播从来没有平均分配。每次遇到一共就买3个不值钱的账号，非要在第一天、第三天、第七天分别释放的思路，我都觉得是个神人。ALL IN都砸不出什么的，怎么还匀匀呢。

说得更加深入一点，帕累托法则的实质是：开始微妙的优势会随着时间逐步加强，最后就能占领绝对优势。“绝大部分的豌豆是由园子里极少部分豌豆荚产生”，不是平白无故的。

公关一定要深刻理解“起始”、“微弱”、“时间”、“逐步”、“绝对”之间的互相作用。

06长尾理论

长尾理论由《连线》杂志主编克里斯·安德森提出，最初用来描述诸如亚马逊和Netflix之类网站的商业和经济模式。作为烂大街理论，每个渠道销售，想推什么卖不出去的东西，都会跟你说一套长尾理论。

长尾理论的本来意思是，只要产品的存储和流通的渠道足够大，需求不旺或销量不佳的产品所共同占据的市场份额可以和那些少数热销产品所占据的市场份额相匹敌甚至更大，即众多小市场汇聚成可产生与主流相匹敌的市场能量。亚马逊是最好用的例子：一家大型书店通常可摆放10万本书，但亚马逊网络书店的图书销售额中，有四分之一来自排名10万以后的书籍。这些“冷门”书籍的销售比例正以高速成长，预估未来可占整个书市的一半。这意味着消费者在面对无限的选择时，真正想要的东西、和想要取得的渠道都出现了重大的变化。

“长尾”实际上是统计学中幂律和帕累托分布特征的一个口语化表达。

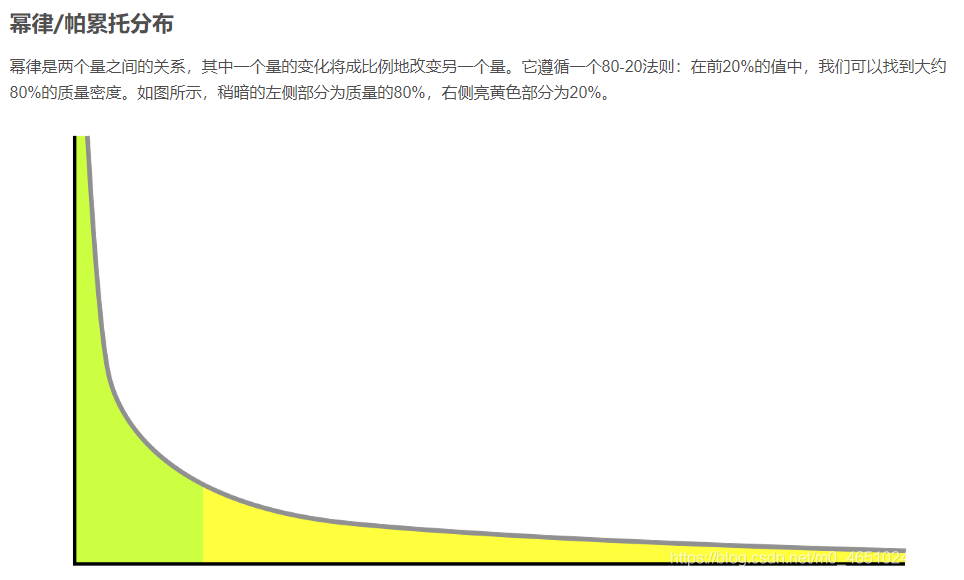
对，这里的帕累托就是上一趴搞出帕累托法则的帕累托。但是，长尾理论其实跟二八法则是相逆的。二八法则劝你关注顶尖儿，长尾理论让你多看看后面的。

理论都是对的，就看应用场景。即便牛顿定律，相对论，量子力学也是如此。长尾理论成立有很多先决条件，二八法则相对比较具有普遍性。

长尾理论对于需要进行渠道采买的市场营销方向同学来说，用起来比较简单。对于公关来说，可能有点烧脑。

因为营销同学在意的长尾，扩充的是品种和来源，排名10万以后的书籍，卖一本算一本，每一本对于收入效果都是一样的。

公关和长尾理论的矛盾在于：传播需要集中话题，打出波峰，叠加热度，诱发自传播。所以，1条帖子获得100个回复，和100个帖子都获得1个回复，完全不是一回事情；1个月获得100万阅读量，和10个月都获得10万阅读量，也完全不是一回事情。

那么，公关就不要长尾了么？也不是。

如果观察鸿星尔克的捐款爆红，你会发现是发生在长尾时期。白象方便面也是。长尾相当于留下了活口，在“引”了之后能“爆”。

注意，企业爆红和素人爆红有本质区别。素人是有可能在之前完全一片白纸，没有任何可以考古素材的前提下，就红了。对于企业来说，我没见过这样的例子。都是之前有长期的累积，在集中爆发之后，才有可能给与支撑。

07正太分布

正态分布也叫高斯分布，就是你在课本里曾经学过的那个两头低、中间高然后左右轴对称的钟形曲线。

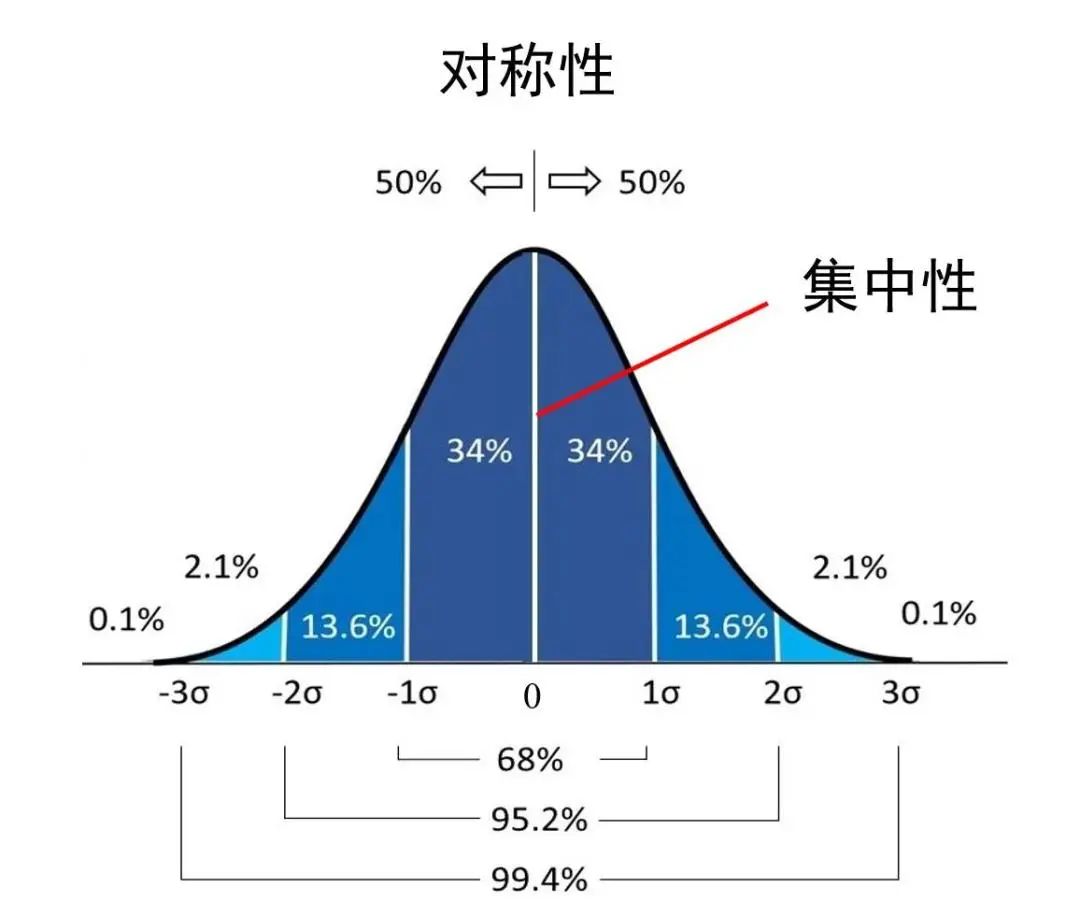
正态分布概念是由法国数学家棣莫弗提出，后由德国数学家高斯率先将其应用于天文学研究。正态分布告诉我们，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布。比如，中国人的平均身高大概是 1 米 7，那么实际上我们随机找 100 个人，把每个区间的身高累个计数画出来一个直方图，它就会是一个正态曲线。除了身高，人来的体重，寿命，胸围等等都符合正态分布规律。

教育统计学发现，学生的智力水平，包括学习能力，实际动手能力等呈正态分布。正常的考试成绩分布，也基本服从正态分布。

医学统计发现，同质群体的身高、红细胞数、血红蛋白量，也呈现为正态或近似正态分布。

作为公关，与做营销最大的区别之一在于，你要面对的不是特定受众，而是广泛公众。正态分布告诉我们，要用整体的观点来看事物，才能看清楚事物的本来面貌，才能得出事物的根本特性。

某一个时刻出现某种舆论，先要判断是偶然的还是该来的来了，是个人瞎逼逼还是这个人承担了“互联网嘴替”，是独角戏还是会被大部分听进去，是独立问题还是连带扯出其他更大的坑。

这是公关的本质，而不是忙着要刊例、找水军、撒钱。

说得绝对一点，没有系统性概念的人是做不了公关的，或者说，做的根本不是公关。

是不是觉得有道理？那我告诉你上面的话存在巨大BUG。

因为正态分布必须满足“一个量是由许多微小的独立随机因素影响”。也就是说，一旦不存在独立性，正态分布就会被破坏。怎么说呢，如果你还记得我说的第一条“信息茧房”，传播上追求独立性几乎都要成为笑话了。

好，准备好，我要放大招了，如果人类的脑力水平是正态分布的，但观点呈现是极端和偏离性质的占据主要声量，说明什么？说明，看上去很绝对的主张并不是我们以为的最脑残的人发出来的。为了符合传播规律和获得更多流量也好、话语权也好、经济利益也好，观点被释放出来，并被广泛接受和传递。

怎么说呢，如果你学会了理论与理论的叠加，得出的结论或许会更可怕。